Keywords:
reconstruction, cone beam CT, noise, beam hardening, scatter
Data degradations including quantum noise, beam hardening and scatter remain a major issue in preclinical/clinical applications, despite the recent advances in x-ray computed tomography. Substantial efforts have been devoted to address individual degradations, however, little attention has been paid to minimize the adverse effects in a unified fashion. In this paper, we combine image reconstruction and artifact reduction in a physics-based synergistic framework. Simulation results showed that less than 10 HU error could be achieved with the proposed framework. Real data experiments showed that the corrected reconstructions with the proposed method exhibited comparable CT values and noise levels as the associated planning CT images.
- Ti Bai
- Institute of Image Processing and Pattern Recognition, Xi'an Jiaotong University, China
- Xuanqin Mou
- Institute of Image Processing and Pattern Recognition, Xi'an Jiaotong University, China
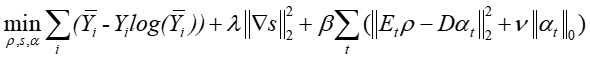
The 3D dictionary learning based sparse representation technique was adopted as the regularizer.
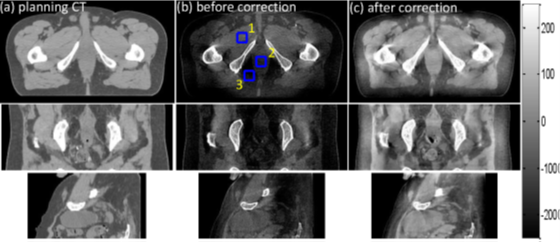
Correction results for the prostate patient case. (a) (c) correspond to the images of the planning CT, before correction and after correction, respectively. Three ROIs as indicated by the blue rectangles in the middle column are selected to calculate the CT values. Display window: [-250 250] HU.
- J. Wang, T. Li, H. Lu, and Z. Liang, “Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for lowdose x-ray computed tomography,” Medical Imaging, IEEE Transactions on, vol. 25, no. 10, pp. 1272–1283, 2006.
- I. A. Elbakri and J. A. Fessler, “Statistical image reconstruction for polyenergetic x-ray computed tomography,” Medical Imaging IEEE Transactions on, vol. 21, no. 2, pp. 89 – 99, 2002.
- E. Sidky and X. Pan, “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Physics in medicine and biology, vol. 53, no. 17, p. 4777, 2008.
- Q. Xu, H. Yu, X. Mou, L. Zhang, J. Hsieh, and G. Wang, “Low-dose x-ray ct reconstruction via dictionary learning,” Medical Imaging, IEEE Transactions on, vol. 31, no. 9, pp. 1682–1697, 2012.
- W. D. Mcdavid, R. G. Waggener, W. H. Payne, and M. J. Dennis, “Correction for spectral artifacts in cross-sectional reconstruction from x rays.” Medical Physics, vol. 4, no. 1, pp. 54–57, 1977.
- P. M. Joseph and R. D. Spital, “A method for correcting bone induced artifacts in computed tomography scanners.” Journal of Computer Assisted Tomography, vol. 2, no. 2, pp. 100–8, 1978.
- J. H. Siewerdsen and D. A. Jaffray, “Cone-beam computed tomography with a flat-panel imager: Magnitude and effects of x-ray scatter,” Medical Physics, vol. 28, no. 2, pp. 220–231, 2001.
- L. Zhu, N. R. Bennett, and R. Fahrig, “Scatter correction method for x-ray ct using primary modulation: Theory and preliminary results,” Medical Imaging, IEEE Transactions on, vol. 25, no. 12, pp. 1573– 1587, 2006.
- P. Wu, X. Sun, H. Hu, T. Mao, W. Zhao, K. Sheng, A. A. Cheung, and T. Niu, “Iterative ct shading correction with no prior information,” Physics in Medicine and Biology, vol. 60, no. 21, p. 8437, 2015.
- Y. Xu, T. Bai, H. Yan, L. Ouyang, A. Pompos, J. Wang, L. Zhou, S. B. Jiang, and X. Jia, “A practical cone-beam ct scatter correction method with optimized monte carlo simulations for image-guided radiation therapy,” Physics in Medicine & Biology, vol. 60, no. 9, pp. 3567–3587, 2015.
- W. Zhao, S. Brunner, K. Niu, S. Schafer, K. Royalty, and G. H. Chen, “Patient-specific scatter correction for flat-panel detector-based conebeam ct imaging,” Physics in Medicine & Biology, vol. 60, no. 3, pp. 1339–1365(27), 2015.
- T. Bai, H. Yan, F. Shi, X. Jia, Y. Lou, Q. Xu, S. B. Jiang, and X. Mou, “We-g-18a-04: 3d dictionary learning based statistical iterative reconstruction for low-dose cone beam ct imaging,” Medical Physics, vol. 41, no. 6, pp. 527–527, 2014.
- L. Feldkamp, L. Davis, and J. Kress, “Practical cone-beam algorithm,” JOSA A, vol. 1, no. 6, pp. 612–619, 1984.
- [Online]. Available: http://physics.nist.gov/PhysRefData/XrayMassCoef/tab2.html
- X. Jia, H. Yan, L. Cervino, M. Folkerts, and S. B. Jiang, “A gpu tool for efficient, accurate, and realistic simulation of cone beam ct projections,” Medical Physics, vol. 39, no. 12, pp. 7368–7378, 2012.
- M. Sun, T. Nagy, G. Virshup, L. Partain, M. Oelhafen, and J. Star-Lack, “Correction for patient table-induced scattered radiation in cone-beam computed tomography (cbct)a),” Medical Physics, vol. 38, no. 4, pp. 2058–2073, 2011.
- H. Y. H. Y. Ti Bai, Xuanqin Mou and G. Wang, “A unified x-ray computed tomographic reconstruction framework,” in The 4th International Conference on Image Formation in X-Ray Computed Tomography, 2016, pp. 165–168.