Keywords:
dictionary learning, sparse representation, low-dose CT, cone-beam CT, noise suppression, GPU
Despite the rapid developments of x-ray cone-beam CT (CBCT), image noise still remains a major issue for the low-dose CBCT. Iterative reconstruction algorithms with 2D dictionary learning (DL) were validated for fine structures and suppressed noise in the case of low-dose CT reconstruction. However, an enhanced version for volumetric CBCT is absent. Besides, it is recognized that representation efficiencies of the sparsity-promotion regularizers are of primary importance for the success of the image processing tasks. In this work, a sparse constraint based on the 3D dictionary is incorporated into a statistical iterative reconstruction, defining the 3D-DL reconstruction framework. From a statistical viewpoint, the distributions of the representation coefficients associated with the 2D/3D dictionaries are analyzed to compare their efficiencies in representing volumetric images. The whole program is implemented on graphic processor units (GPU) to boost the computation efficiency. Experiments demonstrated that the 3D dictionary allows a much higher representation efficiency and a better image quality compared to the 2D dictionary case. Regarding the tested radiation therapy datasets, with a volume of 512×512×512 and a projection dataset of 512×384×363, the whole reconstruction process can be finished within 5 minutes.
- Ti Bai
- Institute of Image Processing and Pattern Recognition, Xi'an Jiaotong University, China
- Hao Yan
- Cyber Medical Corporation, China
- Xun Jia
- Department of Radiation Oncology, UT Southwestern Medical Center, USA
- Steve Jiang
- Department of Radiation Oncology, UT Southwestern Medical Center, USA
- Ge Wang
- Biomedical Imaging Center, Rensselaer Polytechnic Institute, USA
- Xuanqin Mou
- Institute of Image Processing and Pattern Recognition, Xi'an Jiaotong University, China

Illustration of 2D (first row) and 3D (second row) dictionary learning based sparse representations.
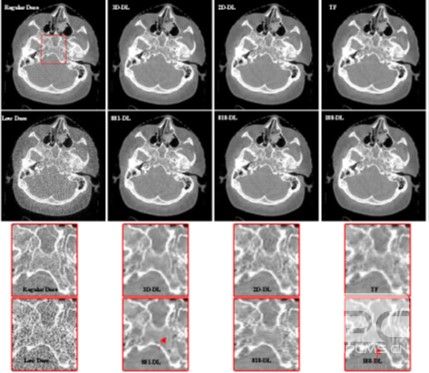
Transversal views of the HN patient images reconstructed by different methods. From left to right in the first row, the images are regular dose FDK reconstruction, reconstructions from the 3D-DL, 2D-DL and TF methods, respectively. From left to right in the second row, the images are reconstructed by the FDK, 881-DL, 818-DL and 188-DL methods, respectively. The last two rows show the corresponding zoomed-in ROIs of the red box in the first two rows. The display window is [-750 750] HU.
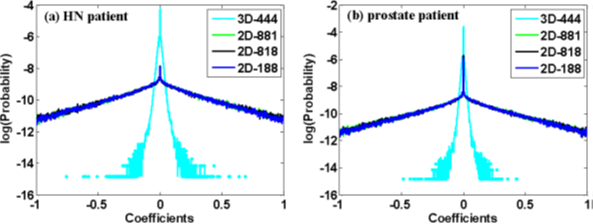
Distributions of the representation coefficients among different dictionaries for the HN patient (a) and prostate patient (b). The x-axis is the values of the coefficients, the y-axis is the logarithmic probabilities. 3D-444 denotes the distributions of the coefficients for the 3D data samples represented by the 3D dictionary of dimension 4*4*4. 2D-881/2D-818/2D-188 denote the distributions of the coefficients with the 2D dictionary for the 2D data samples extracted from the transversal/coronal/sagittal views, respectively.
- D. A. Jaffray and J. H. Siewerdsen, “Cone-beam computed tomography with a flat-panel imager: Initial performance characterization,” Medical Physics, vol. 27, no. 6, pp. 1311–1323, 2000.
- D. A. Jaffray, J. H. Siewerdsen, J. W. Wong, and A. A. Martinez, “Flat-panel cone-beam computed tomography for image-guided rt,” International Journal of Radiation Oncologybiologyphysics, vol. 48, no. 3, pp. 194–194, 2000.
- S. Lee, G. L. Gallia, D. D. Reh, S. Schafer, A. Uneri, D. J. Mirota, S. Nithiananthan, Y. Otake, J.W. Stayman, andW. Zbijewski, “Intraoperative c-arm cone-beam ct: Quantitative analysis of surgical performance in skull base surgery,” Laryngoscope, vol. 122, no. 9, p. 19251932, 2012.
- A. S. Wang, J. W. Stayman, Y. Otake, S. Vogt, G. Kleinszig, and J. H. Siewerdsen, “Accelerated statistical reconstruction for c-arm cone-beam ct using nesterov’s method,” Medical Physics, vol. 42, no. 5, pp. 2699–2708, 2015.
- T. Kiljunen, T. Kaasalainen, A. Suomalainen, and M. Kortesniemi, “Dental cone beam ct: A review.” Physica Medica, vol. 31, no. 8, pp. 844–860, 2015.
- C. L. Sang, H. Kyungkim, I. Konchun, M. Hyecho, S. Y. Lee, and H. C. Min, “A flat-panel detector based micro-ct system: performance evaluation for small-animal imaging,” Physics in Medicine and Biology, vol. 48, no. 24, pp. 4173–4185, 2004.
- A. S. Brody, D. P. Frush, W. Huda, and R. L. Brent, “Radiation risk to children from computed tomography.” Pediatrics, vol. 120, no. 3, pp. 677–682, 2007.
- B. Sinnott, E. Ron, and A. B. Schneider, “Exposing the thyroid to radiation: a review of its current extent, risks, and implications.” Endocrine Reviews, vol. 31, no. 5, pp. 756–773, 2010.
- J. Song, Q. H. Liu, G. A. Johnson, and C. T. Badea, “Sparseness prior based iterative image reconstruction for retrospectively gated cardiac micro-ct,” Medical Physics, vol. 34, no. 11, pp. 4476–4483, 2007.
- E. Y. Sidky and X. Pan, “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Physics in Medicine and Biology, vol. 53, no. 17, pp. 4777–4807, 2008.
- G.-H. Chen, J. Tang, and S. Leng, “Prior image constrained compressed sensing (piccs): a method to accurately reconstruct dynamic ct images from highly undersampled projection data sets,” Medical Physics, vol. 35, no. 2, pp. 660–663, 2008.
- Q. Xu, H. Yu, X. Mou, L. Zhang, J. Hsieh, and G. Wang, “Low-dose x-ray ct reconstruction via dictionary learning,” IEEE Transactions on Medical Imaging, vol. 31, no. 9, pp. 1682–1697, 2012.
- J. Wang, T. Li, Z. Liang, and L. Xing, “Dose reduction for kilovotage cone-beam computed tomography in radiation therapy,” Physics in Medicine and Biology, vol. 53, no. 11, pp. 2897–2909, 2008.
- X. Jia, Y. Lou, R. Li, W. Y. Song, and S. B. Jiang, “Gpu-based fast cone beam ct reconstruction from undersampled and noisy projection data via total variation,” Medical Physics, vol. 37, no. 4, pp. 1757–1760, 2010.
- D. L. Donoho, “Compressed sensing,” IEEE Transactions on Information Theory, vol. 52, no. 4, pp. 1289–1306, 2006.
- G. Yu, L. Li, J. Gu, and L. Zhang, “Total variation based iterative image reconstruction,” Proc. Computer Vision for Biomedical Image Applications: First International Workshop, vol. 3765, pp. 526–534, 2005.
- E. Sidky, C. Kao, and X. Pan, “Accurate image reconstruction from few-views and limited-angle data in divergent-beam ct,” Journal of Xray Science and Technology, vol. 14, no. 2, pp. 119–139, 2006.
- X. Jia, B. Dong, Y. Lou, and S. B. Jiang, “Gpu-based iterative cone-beam ct reconstruction using tight frame regularization.” Physics in Medicine and Biology, vol. 56, no. 13, pp. 3787–3807, 2011.
- M. Aharon, M. Elad, and A. Bruckstein, “K-svd : An algorithm for designing overcomplete dictionaries for sparse representation,” IEEE Transactions on Signal Processing, vol. 54, no. 11, pp. 4311–4322, 2006.
- J. P. Li L, Chen Z, “Dual-energy ct reconstruction based on dictionary learning and total variation constraint,” in Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), 2012 IEEE, pp. 2358–2361.
- B. A. Olshausen and D. J. Field, “Emergence of simple-cell receptive field properties by learning a sparse code for natural images.” Nature, vol. 381, no. 6583, pp. 607–609, 1996.
- M. S. Lewicki and T. J. Sejnowski, “Learning overcomplete representations.” Neural Computation, vol. 12, no. 2, pp. 337–365, 2000.
- Q. Liu, S. Wang, and J. Luo, “A novel predual dictionary learning algorithm,” Journal of Visual Communication and Image Representation, vol. 23, no. 1, pp. 182–193, 2012.
- I. A. Elbakri and J. A. Fessler, “Statistical image reconstruction for polyenergetic x-ray computed tomography,” IEEE Transactions on Medical Imaging, vol. 21, no. 2, pp. 89 – 99, 2002.
- J. Wang, H. Lu, Z. Liang, D. Eremina, G. Zhang, S. Wang, J. Chen, and J. Manzione, “An experimental study on the noise properties of xray ct sinogram data in radon space,” Physics in Medicine and Biology, vol. 53, no. 12, pp. 3327–3341, 2008.
- H. Y. J. Wu, X. Mou and G. Wang, “Statistical interior tomography via dictionary learning without assuming an object support,” Proc. Fully3D, pp. 440–443, 2013.
- X. Mou, J. Wu, Q. Xu, H. Yu, and G. Wang, “Dictionary learning based low-dose x-ray ct reconstruction using a balancing principle,” Proc. SPIE, vol. 9212, pp. 921 207–921 207–15, 2014.
- J. Huang and D. Mumford, “Statistics of natural images and models,” cvpr, p. 1541, 1999.
- N. Y., “A method for unconstrained convex minimization problem with the rate of convergence o (1/k2),” Doklady an SSSR, vol. 269, no. 3, pp. 543–547, 1983.
- J. H. Cho and J. A. Fessler, “Accelerating ordered-subsets image reconstruction for x-ray ct using double surrogates,” Proc. SPIE, vol. 8313, no. 2, pp. 145–150, 2012.
- D. Needell and J. A. Tropp, “Cosamp: Iterative signal recovery from incomplete and inaccurate samples,” Applied and Computational Harmonic Analysis, vol. 26, no. 3, pp. 301–321, 2009.
- D. L. Donoho, Y. Tsaig, I. Drori, and J. L. Starck, “Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit,” IEEE Transactions on Information Theory, vol. 58, no. 2, pp. 1094 -1121, 2006.
- T. Goldstein and S. Osher, “The split bregman method for l1-regularized problems,” SIAM Journal on Imaging Sciences, vol. 2, no. 2, pp. 323– 343, 2009.
- B. L. Sturm and M. G. Christensen, “Comparison of orthogonal matching pursuit implementations,” Proc. the 20th European Signal Processing Conference.
- Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, “Image quality assessment: from error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004.
- J. P. Jones and L. A. Palmer, “The two-dimensional spectral structure of simple receptive fields in cat striate cortex.” Journal of Neurophysiology, vol. 58, no. 58, pp. 1212–32, 1987.
- D. J. Field, “Relations between the statistics of natural images and the response properties of cortical cells.” Journal of the Optical Society of America A Optics and Image Science, vol. 4, no. 4, pp. 2379–2394, 1987.